A I Escola em Dinâmica tem o objetivo de oferecer aos alunos conhecimentos fundamentais, atuais e avançados relacionados à área de dinâmica. O plano de estudos é composto por 5 módulos conforme apresentado abaixo.
DIN01 – Dinâmica Clássica.
DIN02 – Mecânica Analítica.
VIB – Vibração de Sistemas Mecânicos.
DIN-NL – Dinâmica Não-Linear e Caos.
DIN-ST – Dinâmica Estocástica.
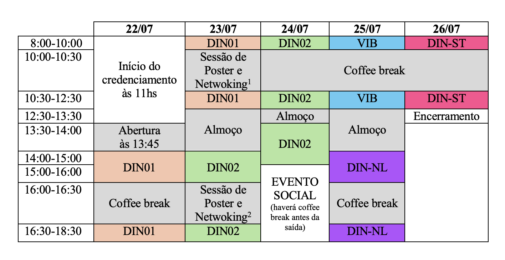
PROGRAMAÇÃO
Relação dos títulos dos pôsteres a serem apresentados no dia 23/07 às 10h00:
|
|
|
|
|
|
Relação dos títulos dos pôsteres a serem apresentados no dia 23/07 às 16h00:
|
|
|
|
|
INFORMAÇÕES DETALHADAS DOS MÓDULOS
DIN01
Dinâmica Clássica
Professor: Ilmar Santos (DTU-Dinamarca)

Tópicos:
- Dinâmica de Partículas e Sistemas de Partículas (4 horas)
Sistemas de referência, matrizes de transformação de coordenadas, vetores de posição, velocidade, e aceleração, equilíbrio dinâmico, equações de movimento e de reações dinâmicas, métodos numéricos para a solução das equações de movimento e reações dinâmicas, exemplos de aplicação em 2D e 3D.
- Dinâmica de Corpos Rígidos e Sistemas de Corpos Rígidos (4 horas)
Sistemas de referência, matrizes de transformação de coordenadas, vetores de posição, velocidade, e aceleração, momentos de inércia, equilíbrio dinâmico, equações de movimento e de reações dinâmicas, exemplos de aplicação em 2D e 3D.
Referência:
- I F Santos. (2000) Dinâmica de Sistemas Mecânicos – Modelagem, Simulação, Visualização, Verificação, Makron Books Ltda., ISBN 85-346-1110-6.
DIN02
Mecânica Analítica
Professor: Celso Pesce (USP)

Tópicos:
- Introdução.
- Apresentação das Equações de Lagrange. Vínculos. Graus de Liberdade. Coordenadas Generalizadas. Deslocamentos Possíveis. Deslocamentos Virtuais.
- Trabalho Virtual.
- Princípio dos Trabalhos Virtuais.
- Dedução das Equações de Lagrange para Sistemas Holônomos.
- Equações de Lagrange e Sistemas Conservativos.
- Sistemas Dissipativos Rayleighianos.
- Funcionais e variação de um funcional.
- Estacionariedade.
- Equação de Euler.
- O Princípio de D’Alembert e o Princípio de Hamilton.
- As Equações de Lagrange – sistemas holônomos e não-holônomos.
- Transformação de Legendre.
- Equações Canônicas de Hamilton.
- Integral Canônica.
- Coordenadas cíclicas e Método de Routh.
- Integral de Jacobi.
- As Equações de Lagrange para Sistemas de Massa Variável.
Referências:
- Lanczos, C., The Variational Principles of Mechanics, Dover, 1986.
- Gelfand, I.M., Fomin, S.V., Calculus of Variations. Dover, 1991.
- Meirovitch, L., Methods of Analytical Dynamics, McGraw-Hill, 1988.
- Hamill, P. A Student’s Guide to Lagrangians and Hamiltonians. Cambridge University Press, 2014.
- Neuenschwander, D.E., Emmy Noether’s Wonderful Theorem, Johns Hopkins University Press, 2017.
- Pesce, C.P., Casetta, L. Systems with mass explicitly dependent on position. In: Dynamics of Mechanical Systems with Variable Mass.1sted.: Springer, 2014, v.557, p. 51-106.
VIB
DIN-NL
Dinâmica Não-Linear e Caos
Professor: Marcelo Savi (COPPE/UFRJ).

Objetivos gerais:
A natureza está repleta de não-linearidades que são responsáveis pela diversidade de comportamentos dos sistemas naturais. O comportamento caótico possui uma sensibilidade às condições iniciais, o que implica que a evolução do sistema pode ser alterada por pequenas perturbações. Além disso, a estrutura de uma resposta caótica é muito rica, estando associada a uma infinidade de órbitas periódicas instáveis. Essas propriedades fazem com que o comportamento caótico possua uma grande flexibilidade, sendo interessante para sistemas que necessitam apresentar uma reação rápida a determinadas perturbações. Este minicurso tem como objetivo fazer uma introdução as sistemas dinâmicos não-lineares, dando uma atenção especial ao comportamento caótico
Tópicos:
- Introdução
Revisão histórica; Sistemas físicos não-lineares.
- Fundamentação Teórica
Sistemas dinâmicos; Espaço de fase; Mapa de Poincaré; Equivalência topológica; Estabilidade; Linearização; Pontos de equilíbrio; Variedades; Comportamento assintótico.
- Teoria do Caos
Transformação da ferradura; Conjunto de Cantor; Dimensão fractal; Atratores estranhos e caóticos; Invariantes geométricos; Bifurcações.
- Análise de Séries Temporais
Reconstrução do espaço de estado; Predição; Controle de caos.
Referências:
- Livro Texto: Savi, M.A., “Dinâmica Não-linear e Caos”, Editora E-papers, 2017.
- Bibliografia Complementar
- El Nachie, M.S., “Stress, Stability & Chaos in Structural Engineering”, McGraw Hill, 1992.
- Gleick, J., “Caos”, Campus, Rio de Janeiro, 1987.
- Guckenheimer, J. & Holmes, P., “Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields”, Springer-Verlag, New York, 1983.
- Kapitaniak, T., “Chaotic Oscillations in Mechanical Systems”, Manchester, 1991.
- Moon, F., “Chaotic and Fractal Dynamics”, John Wiley & Sons, New York, 1992.
- Nayfeh, A.H. & Mook, D.T., “Nonlinear Oscillations”, John Wiley & Sons, 1979.
- Ott, E., “Chaos in Dynamical Systems”, Cambridge Press, 1993.
- Savi, M.A., “Ritmos da Natureza”, Editora E-papers, 2014.
- Schuster, H.G., “Deterministic Chaos”, VCH, 1989.
- Stewart, I., “Será que Deus Joga Dados? A Nova Matemática do Caos”, Jorge Zahar Editor, 1991.
- Strogatz, S.H., “Nonlinear Dynamics and Chaos”, Perseus, 1994.
- Thompsom, J.M.T & Stewart, H.B., “Nonlinear Dynamics and Chaos”, John Wiley & Sons, Chichester, 1986.
- Wiggins, S., “Introduction to Applied Nonlinear Dynamical Systems and Chaos”, Springer-Verlag, New York, 1990.
Material complementar:
DIN-ST
Dinâmica Estocástica
Professora: Roberta Lima (PUC-RJ)

Tópicos:
- Exemplos de incertezas em problemas de dinâmica.
- Conceitos báasicos: espaço de probabilidade, objetos aleatórios (variáveis aleatórias discretas e contínuas, vetores aleatórios e processos estocásticos), estatísticas.
- Transformação de objetos aleatórios.
- Geração de amostras de variáveis e vetores aleatórios.
- Construção de um modelo estatístico: estimadores de estatísticas e histogramas.
- Método de Monte Carlo.
- Discussão sobre o que é quantificação de incerteza e uso de estatísticas para medir incerteza.
- Discussão sobre o que é propagação de incertezas.
Referências:
- R. Sampaio e R. Lima R. Modelagem estocástica e geração de amostras de variáveis e vetores aleatórios. Notas em Matemática Aplicada, Sociedade Brasileira de Matemática Aplicada e Computacional (SBMAC), São Carlos, volume 70, 2012. Download gratuito: https://www.sbmac.org.br/wp-content/uploads/2022/08/livro_70.pdf
- R. Lima e R. Sampaio. What is uncertainty quantification? Journal of the Brazilian Society of Mechanical Sciences and Engineering, v. 40, p. 155, 2018.